If the G of a Reaction Was -31.45kjoules You Know That

Affiliate xvi. Thermodynamics

xvi.four Costless Energy

Learning Objectives

By the end of this section, you volition be able to:

• Ascertain Gibbs free energy, and describe its relation to spontaneity
• Summate free free energy change for a procedure using free energies of formation for its reactants and products
• Calculate gratis energy alter for a process using enthalpies of formation and the entropies for its reactants and products
• Explain how temperature affects the spontaneity of some processes
• Relate standard free free energy changes to equilibrium constants

One of the challenges of using the second constabulary of thermodynamics to determine if a procedure is spontaneous is that we must determine the entropy change for the arrangement and the entropy modify for the surroundings. An alternative arroyo involving a new thermodynamic belongings defined in terms of system properties simply was introduced in the late nineteenth century past American mathematician Josiah Willard Gibbs. This new property is called the Gibbs complimentary energy change (G) (or just the free energy), and it is divers in terms of a system's enthalpy and entropy every bit the following:

[latex]G = H\;-\;TS[/latex]

Costless free energy is a state function, and at abiding temperature and pressure, the standard gratuitous energy change (ΔG°) may exist expressed as the following:

[latex]{\Delta}Thousand = {\Delta}H\;-\;T{\Delta}Southward[/latex]

(For simplicity's sake, the subscript "sys" volition be omitted henceforth.)

We can empathize the relationship between this arrangement property and the spontaneity of a process by recalling the previously derived second constabulary expression:

[latex]{\Delta}S_{\text{univ}} = {\Delta}S\;+\;\frac{q_{\text{surr}}}{T}[/latex]

The offset law requires that q _surr = −q _sys, and at constant force per unit area q _sys = ΔH, and so this expression may exist rewritten as the following:

[latex]{\Delta}S_{\text{univ}} = {\Delta}Due south\;-\;\frac{{\Delta}H}{T}[/latex]

ΔH is the enthalpy alter of the system. Multiplying both sides of this equation by −T, and rearranging yields the following:

[latex]-T{\Delta}S_{\text{univ}} = {\Delta}H\;-\;T{\Delta}S[/latex]

Comparing this equation to the previous 1 for complimentary energy modify shows the following relation:

[latex]{\Delta}1000 = -T{\Delta}S_{\text{univ}}[/latex]

The free energy change is therefore a reliable indicator of the spontaneity of a procedure, existence direct related to the previously identified spontaneity indicator, ΔSouth _univ. Tabular array 3 summarizes the relation between the spontaneity of a process and the arithmetics signs of these indicators.

ΔDue south univ > 0	ΔChiliad < 0	spontaneous
ΔS univ < 0	ΔThousand > 0	nonspontaneous
ΔS univ = 0	ΔG = 0	reversible (at equilibrium)
Table 3. Relation between Process Spontaneity and Signs of Thermodynamic Properties

Calculating Gratis Free energy Change

Gratis energy is a state function, and then its value depends only on the weather of the initial and final states of the arrangement that have undergone some change. A convenient and common approach to the calculation of free energy changes for physical and chemical reactions is by use of widely bachelor compilations of standard state thermodynamic data. I method involves the apply of standard enthalpies and entropies to compute standard free energy changes according to the post-obit relation as demonstrated in Case one.

[latex]{\Delta}G^{\circ} = {\Delta}H^{\circ}\;-\;T{\Delta}S^{\circ}[/latex]

Instance i

Evaluation of ΔG° Change from ΔH° and ΔSouthward°
Use standard enthalpy and entropy data from Appendix G to calculate the standard free energy change for the vaporization of water at room temperature (298 K). What does the computed value for ΔG° say nearly the spontaneity of this procedure?

Solution
The process of involvement is the post-obit:

[latex]\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{H}_2\text{O}(g)[/latex]

The standard change in free free energy may be calculated using the following equation:

[latex]{\Delta}G_{298}^{\circ} = {\Delta}H^{\circ}\;-\;T{\Delta}South^{\circ}[/latex]

From Appendix G, here is the data:

Substance	[latex]{\Delta}H_{\text{f}}^{\circ}(\text{kJ/mol})[/latex]	[latex]S_{298}^{\circ}(\text{J/K}{\cdot}\text{mol})[/latex]
H2O(l)	−286.83	seventy.0
HiiO(g)	−241.82	188.8
Table 4.

Combining at 298 K:

[latex]{\Delta}H^{\circ} = {\Delta}H_{298}^{\circ} = {\Delta}H_{\text{f}}^{\circ}(\text{H}_2\text{O}(thousand))\;-\;{\Delta}H_{\text{f}}^{\circ}(\text{H}_2\text{O}(50)) = [-241.82\;\text{kJ}\;-\;(-285.83)]\text{kJ/mol} = 44.01\;\text{kJ/mol}[/latex]

[latex]{\Delta}South^{\circ} = {\Delta}S_{298}^{\circ} = S_{298}^{\circ}(\text{H}_2\text{O}(k))\;-\;S_{298}^{\circ}(\text{H}_2\text{O}(l)) = 188.8\;\text{J/mol}{\cdot}\text{K}\;-\;70.0\text{J/Thou} = 118.8\;\text{J/mol}{\cdot}\text{K}[/latex]

[latex]{\Delta}G^{\circ} = {\Delta}H^{\circ}\;-\;T{\Delta}Due south^{\circ}[/latex]

Converting everything into kJ and combining at 298 K:

[latex]\begin{array}{r @{{}={}} l} {\Delta}G_{298}^{\circ} & {\Delta}H^{\circ}\;-\;T{\Delta}S^{\circ} \\[0.5em] & 44.01\;\text{kJ/mol}\;-\;(298\;\text{K}\;\times\;118.8\;\text{J/mol}{\cdot}\text{K})\;\times\;\frac{one\;\text{kJ}}{chiliad\;\text{J}} \end{assortment}[/latex]

[latex]44.01\;\text{kJ/mol}\;-\;35.iv\;\text{kJ/mol} = 8.6\;\text{kJ/mol}[/latex]

At 298 K (25 °C) [latex]{\Delta}G_{298}^{\circ}\;{\textgreater}\;0[/latex], and so boiling is nonspontaneous (non spontaneous).

Check Your Learning
Utilise standard enthalpy and entropy information from Appendix K to calculate the standard costless energy change for the reaction shown hither (298 K). What does the computed value for ΔG° say about the spontaneity of this process?

[latex]\text{C}_2\text{H}_6(g)\;{\longrightarrow}\;\text{H}_2(g)\;+\;\text{C}_2\text{H}_4(thou)[/latex]

Answer:

[latex]{\Delta}G_{298}^{\circ} = 102.0\;\text{kJ/mol}[/latex]; the reaction is nonspontaneous (not spontaneous) at 25 °C.

Free energy changes may also use the standard gratis energy of germination ([latex]{\Delta}G_{\text{f}}^{\circ}[/latex]), for each of the reactants and products involved in the reaction. The standard gratis energy of germination is the gratis energy change that accompanies the formation of one mole of a substance from its elements in their standard states. Similar to the standard enthalpies of formation, [latex]{\Delta}G_{\text{f}}^{\circ}[/latex] is by definition zero for elemental substances under standard state atmospheric condition. The approach to calculating the costless energy change for a reaction using this approach is the aforementioned as that demonstrated previously for enthalpy and entropy changes. For the reaction

[latex]m\text{A}\;+\;n\text{B}\;{\longrightarrow}\;x\text{C}\;+\;y\text{D}[/latex],

the standard free free energy change at room temperature may be calculated as

[latex]{\Delta}G_{298}^{\circ} = {\Delta}One thousand^{\circ} = {\sum}five{\Delta}G_{298}^{\circ}(\text{products})\;-\;{\sum}v{\Delta}G_{298}^{\circ}(\text{reactants}) = [x{\Delta}G_{\text{f}}^{\circ}(\text{C})\;+\;y{\Delta}G_{\text{f}}^{\circ}(\text{D})]\;-\;[thousand{\Delta}G_{\text{f}}^{\circ}(\text{A})\;+\;n{\Delta}G_{\text{f}}^{\circ}(\text{B})][/latex].

Example 2

Calculation of [latex]{\Delta}G_{298}^{\circ}[/latex]
Consider the decomposition of yellow mercury(2) oxide.

[latex]\text{HgO}(s\text{,\;yellow})\;{\longrightarrow}\;\text{Hg}(l)\;+\;\frac{1}{2}\text{O}_2(g)[/latex]

Calculate the standard free energy alter at room temperature, [latex]{\Delta}G_{298}^{\circ}[/latex], using (a) standard free energies of formation and (b) standard enthalpies of germination and standard entropies. Do the results indicate the reaction to be spontaneous or nonspontaneous under standard atmospheric condition?

Solution
The required data are available in Appendix G and are shown here.

Compound	[latex]{\Delta}G_{\text{f}}^{\circ}(\text{kJ/mol})[/latex]	[latex]{\Delta}H_{\text{f}}^{\circ}(\text{kJ/mol})[/latex]	[latex]S_{298}^{\circ}(\text{J/M}{\cdot}\text{mol})[/latex]
HgO (southward, yellow)	−58.43	−90.46	71.13
Hg(l)	0	0	75.nine
O2(k)	0	0	205.ii
Tabular array v.

(a) Using gratuitous energies of formation:

[latex]{\Delta}G_{298}^{\circ} = {\sum}vGS_{298}^{\circ}(\text{products})\;-\;{\sum}vGS_{298}^{\circ}(\text{reactants})[/latex]

[latex]= [1{\Delta}G_{298}^{\circ}\text{Hg}(50)\;+\;\frac{1}{ii}{\Delta}G_{298}^{\circ}\text{O}_2(g)]\;-\;i{\Delta}G_{298}^{\circ}\text{HgO}(s\text{,\;yellow})[/latex]

[latex]= [one\;\text{mol}(0\;\text{kJ/mol})\;+\;\frac{1}{2}\text{mol}(0\;\text{kJ/mol})]\;-\;1\;\text{mol}(-58.43\;\text{kJ/mol}) = 58.43\;\text{kJ/mol}[/latex]

(b) Using enthalpies and entropies of formation:

[latex]{\Delta}H_{298}^{\circ} = {\sum}v{\Delta}H_{298}^{\circ}(\text{products})\;-\;{\sum}5{\Delta}H_{298}^{\circ}(\text{reactants})[/latex]

[latex]= [1{\Delta}H_{298}^{\circ}\text{Hg}(fifty)\;+\;\frac{1}{2}{\Delta}H_{298}^{\circ}\text{O}_2(g)]\;-\;1{\Delta}H_{298}^{\circ}\text{HgO}(s\text{,\;yellowish})[/latex]

[latex]= [1\;\text{mol}(0\;\text{kJ/mol})\;+\;\frac{one}{2}\text{mol}(0\;\text{kJ/mol})]\;-\;1\;\text{mol}(-90.46\;\text{kJ/mol}) = 90.46\;\text{kJ/mol}[/latex]

[latex]{\Delta}S_{298}^{\circ} = {\sum}v{\Delta}S_{298}^{\circ}(\text{products})\;-\;{\sum}v{\Delta}S_{298}^{\circ}(\text{reactants})[/latex]

[latex]= [i{\Delta}S_{298}^{\circ}\text{Hg}(50)\;+\;\frac{i}{2}{\Delta}S_{298}^{\circ}\text{O}_2(m)]\;-\;i{\Delta}S_{298}^{\circ}\text{HgO}(south\text{,\;yellow})[/latex]

[latex]= [1\;\text{mol}(75.ix\;\text{J/mol\;Yard})\;+\;\frac{1}{ii}\text{mol}(205.2\;\text{J/mol\;K})]\;-\;1\;\text{mol}(71.xiii\;\text{J/mol\;K}) = 107.four\;\text{J/mol\;K}[/latex]

[latex]{\Delta}G^{\circ} = {\Delta}H^{\circ}\;-\;T{\Delta}Southward^{\circ} = 90.46\;\text{kJ}\;-\;298.xv\;\text{M}\;\times\;107.4\;\text{J/K}{\cdot}\text{mol}\;\times\;\frac{1\;\text{kJ}}{1000\;\text{J}}[/latex]

[latex]{\Delta}1000^{\circ} = (ninety.46\;-\;32.01)\;\text{kJ/mol} = 58.45\;\text{kJ/mol}[/latex]

Both ways to calculate the standard free energy change at 25 °C give the same numerical value (to 3 pregnant figures), and both predict that the process is nonspontaneous (not spontaneous) at room temperature.

Check Your Learning
Calculate Δ1000° using (a) free energies of formation and (b) enthalpies of formation and entropies (Appendix K). Practice the results indicate the reaction to be spontaneous or nonspontaneous at 25 °C?

[latex]\text{C}_2\text{H}_4(thou)\;{\longrightarrow}\;\text{H}_2(one thousand)\;+\;\text{C}_2\text{H}_2(g)[/latex]

Reply:

−141.5 kJ/mol, nonspontaneous

Temperature Dependence of Spontaneity

As was previously demonstrated in this chapter's section on entropy, the spontaneity of a procedure may depend upon the temperature of the organisation. Phase transitions, for instance, volition proceed spontaneously in i direction or the other depending upon the temperature of the substance in question. As well, some chemical reactions can as well exhibit temperature dependent spontaneities. To illustrate this concept, the equation relating free free energy alter to the enthalpy and entropy changes for the process is considered:

[latex]{\Delta}G = {\Delta}H\;-\;T{\Delta}S[/latex]

The spontaneity of a process, equally reflected in the arithmetic sign of its free free energy change, is and so determined by the signs of the enthalpy and entropy changes and, in some cases, the absolute temperature. Since T is the absolute (kelvin) temperature, information technology tin can simply take positive values. 4 possibilities therefore exist with regard to the signs of the enthalpy and entropy changes:

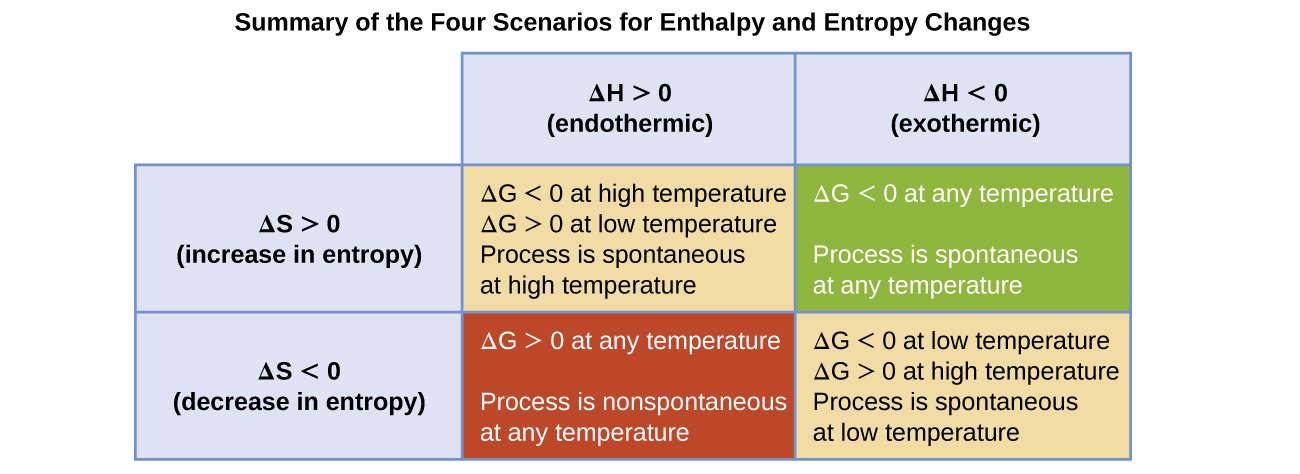
1. Both ΔH and ΔSouth are positive. This condition describes an endothermic process that involves an increase in organisation entropy. In this case, ΔG will be negative if the magnitude of the TΔS term is greater than ΔH. If the TΔS term is less than ΔH, the energy change volition exist positive. Such a procedure is spontaneous at high temperatures and nonspontaneous at depression temperatures.
2. Both ΔH and ΔSouth are negative. This condition describes an exothermic process that involves a decrease in system entropy. In this case, ΔG volition be negative if the magnitude of the TΔS term is less than ΔH. If the TΔS term'southward magnitude is greater than ΔH, the free energy change will be positive. Such a process is spontaneous at low temperatures and nonspontaneous at loftier temperatures.
3. ΔH is positive and ΔSouthward is negative. This condition describes an endothermic process that involves a decrease in arrangement entropy. In this case, ΔG will be positive regardless of the temperature. Such a process is nonspontaneous at all temperatures.
4. ΔH is negative and ΔDue south is positive. This status describes an exothermic process that involves an increase in arrangement entropy. In this case, ΔG will be negative regardless of the temperature. Such a process is spontaneous at all temperatures.

These 4 scenarios are summarized in Figure 1.

Figure one. There are iv possibilities regarding the signs of enthalpy and entropy changes.

Example three

Predicting the Temperature Dependence of Spontaneity
The incomplete combustion of carbon is described past the following equation:

[latex]two\text{C}(s)\;+\;\text{O}_2(1000)\;{\longrightarrow}\;2\text{CO}(g)[/latex]

How does the spontaneity of this procedure depend upon temperature?

Solution
Combustion processes are exothermic (ΔH < 0). This item reaction involves an increase in entropy due to the accompanying increment in the amount of gaseous species (cyberspace gain of one mole of gas, ΔDue south > 0). The reaction is therefore spontaneous (ΔYard < 0) at all temperatures.

Check Your Learning
Popular chemic hand warmers generate heat by the air-oxidation of fe:

[latex]4\text{Fe}(southward)\;+\;3\text{O}_2(1000)\;{\longrightarrow}\;2\text{Fe}_2\text{O}_3(s)[/latex]

How does the spontaneity of this process depend upon temperature?

Answer:

ΔH and ΔS are negative; the reaction is spontaneous at low temperatures.

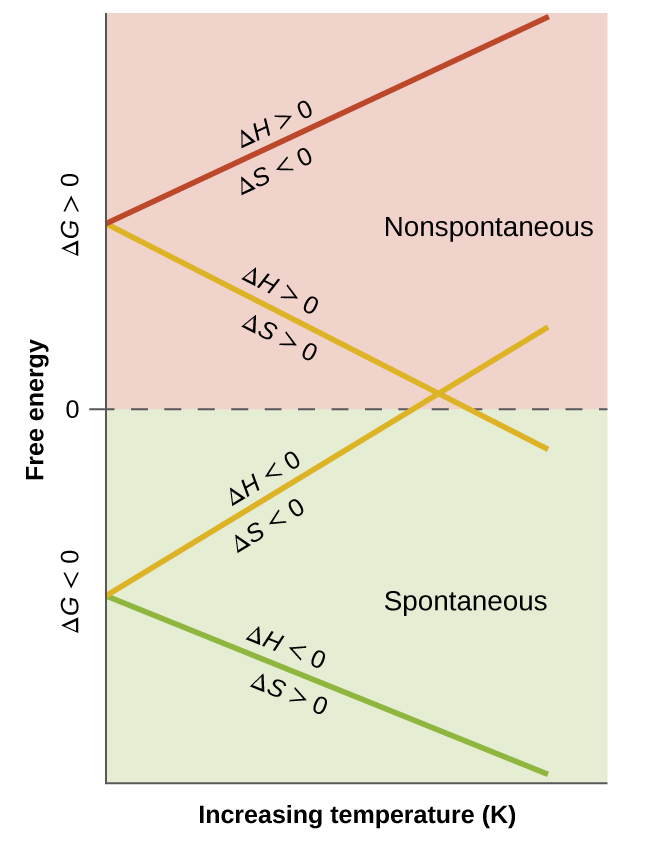
When because the conclusions fatigued regarding the temperature dependence of spontaneity, it is important to keep in mind what the terms "loftier" and "depression" mean. Since these terms are adjectives, the temperatures in question are deemed high or low relative to some reference temperature. A process that is nonspontaneous at one temperature simply spontaneous at some other will necessarily undergo a modify in "spontaneity" (equally reflected by its ΔG) as temperature varies. This is conspicuously illustrated by a graphical presentation of the free energy change equation, in which ΔThou is plotted on the y axis versus T on the 10 axis:

[latex]{\Delta}Grand = {\Delta}H\;-\;T{\Delta}Southward[/latex]

[latex]y = b\;+\;mx[/latex]

Such a plot is shown in Figure two. A process whose enthalpy and entropy changes are of the same arithmetic sign will showroom a temperature-dependent spontaneity as depicted by the two yellow lines in the plot. Each line crosses from 1 spontaneity domain (positive or negative ΔThousand) to the other at a temperature that is feature of the process in question. This temperature is represented by the x-intercept of the line, that is, the value of T for which ΔThousand is nil:

[latex]{\Delta}G = 0 = {\Delta}H\;-\;T{\Delta}S[/latex]

[latex]T = \frac{{\Delta}H}{{\Delta}S}[/latex]

So, saying a process is spontaneous at "high" or "depression" temperatures ways the temperature is above or below, respectively, that temperature at which ΔThousand for the process is zero. As noted earlier, this condition describes a organisation at equilibrium.

Figure 2. These plots bear witness the variation in ΔGrand with temperature for the iv possible combinations of arithmetics sign for ΔH and ΔS.

Example 4

Equilibrium Temperature for a Phase Transition
As defined in the chapter on liquids and solids, the boiling point of a liquid is the temperature at which its solid and liquid phases are in equilibrium (that is, when vaporization and condensation occur at equal rates). Use the information in Appendix Grand to gauge the boiling indicate of water.

Solution
The process of interest is the following phase change:

[latex]\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{H}_2\text{O}(g)[/latex]

When this process is at equilibrium, ΔGrand = 0, then the post-obit is true:

[latex]0 = {\Delta}H^{\circ}\;-\;T{\Delta}S^{\circ}\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;T = \frac{{\Delta}H^{\circ}}{{\Delta}Due south^{\circ}}[/latex]

Using the standard thermodynamic information from Appendix G,

[latex]\begin{assortment}{r @{{}={}} fifty} {\Delta}H^{\circ} & {\Delta}H_{\text{f}}^{\circ}(\text{H}_2\text{O}(thousand))\;-\;{\Delta}H_{\text{f}}^{\circ}(\text{H}_2\text{O}(fifty)) \\[0.5em] & -241.82\;\text{kJ/mol}\;-\;(-285.83\;\text{kJ/mol}) = 44.01\;\text{kJ/mol} \end{array}[/latex]

[latex]\begin{array}{r @{{}={}} l} {\Delta}S^{\circ} & {\Delta}S_{298}^{\circ}(\text{H}_2\text{O}(yard))\;-\;{\Delta}S_{298}^{\circ}(\text{H}_2\text{O}(l)) \\[0.5em] & 188.8\;\text{J/K}{\cdot}\text{mol}\;-\;70.0\;\text{J/Thou}{\cdot}\text{mol} = 118.8\;\text{J/Chiliad}{\cdot}\text{mol} \end{array}[/latex]

[latex]T = \frac{{\Delta}H^{\circ}}{{\Delta}South^{\circ}} = \frac{44.01\;\times\;ten^3\;\text{J/mol}}{118.eight\;\text{J/K}{\cdot}\text{mol}} = 370.five\;\text{Thou} = 97.iii\;^{\circ}\text{C}[/latex]

The accustomed value for h2o'southward normal humid bespeak is 373.2 1000 (100.0 °C), and so this adding is in reasonable understanding. Note that the values for enthalpy and entropy changes data used were derived from standard information at 298 K (Appendix M). If desired, you could obtain more than accurate results by using enthalpy and entropy changes adamant at (or at least closer to) the bodily boiling point.

Check Your Learning
Employ the information in Appendix K to estimate the boiling signal of CS₂.

Answer:

313 Chiliad (accepted value 319 M)

Costless Energy and Equilibrium

The gratuitous energy change for a procedure may be viewed as a measure out of its driving forcefulness. A negative value for ΔThou represents a finite driving force for the process in the forward direction, while a positive value represents a driving force for the process in the reverse management. When ΔGrand is nada, the frontwards and reverse driving forces are equal, then the procedure occurs in both directions at the same charge per unit (the system is at equilibrium).

In the affiliate on equilibrium the reaction quotient, Q, was introduced as a convenient mensurate of the status of an equilibrium system. Remember that Q is the numerical value of the mass activity expression for the system, and that you may use its value to identify the direction in which a reaction volition proceed in social club to achieve equilibrium. When Q is lesser than the equilibrium abiding, K, the reaction will go along in the forward management until equilibrium is reached and Q = 1000. Conversely, if Q < K, the procedure will proceed in the reverse management until equilibrium is accomplished.

The costless free energy change for a process taking place with reactants and products present nether nonstandard conditions, ΔOne thousand, is related to the standard free energy change, ΔG°, co-ordinate to this equation:

[latex]{\Delta}Thou = {\Delta}G^{\circ}\;+\;RT\;\text{ln}\;Q[/latex]

R is the gas constant (viii.314 J/M mol), T is the kelvin or absolute temperature, and Q is the reaction caliber. We may utilize this equation to predict the spontaneity for a procedure under whatsoever given fix of conditions as illustrated in Instance 5.

Example 5

Calculating ΔThou under Nonstandard Conditions
What is the energy change for the process shown here under the specified conditions?

T = 25 °C, [latex]\text{P}_{\text{N}_2} = 0.870\;\text{atm}[/latex], [latex]\text{P}_{\text{H}_2} = 0.250\;\text{atm}[/latex], and [latex]\text{P}_{\text{NH}_3} = 12.9\;\text{atm}[/latex]

[latex]2\text{NH}_3(grand)\;{\longrightarrow}\;3\text{H}_2(1000)\;+\;\text{N}_2(g)\;\;\;\;\;\;\;{\Delta}K^{\circ} = 33.0\;\text{kJ/mol}[/latex]

Solution
The equation relating costless free energy alter to standard energy alter and reaction quotient may be used directly:

[latex]{\Delta}G = {\Delta}Thousand^{\circ}\;+\;RT\;\text{ln}\;Q = 33.0\;\frac{\text{kJ}}{\text{mol}}\;+\;(8.314\;\frac{\text{J}}{\text{mol\;K}}\;\times\;298\;\text{K}\;\times\;\text{ln}\;\frac{(0.250^3)\;\times\;0.870}{12.9^2}) = 9680\;\frac{\text{J}}{\text{mol}}\;\text{or}\;ix.68\;\text{kJ/mol}[/latex]

Since the computed value for ΔG is positive, the reaction is nonspontaneous under these conditions.

Check Your Learning
Summate the free energy change for this aforementioned reaction at 875 °C in a 5.00 50 mixture containing 0.100 mol of each gas. Is the reaction spontaneous under these atmospheric condition?

Reply:

ΔChiliad = −136 kJ; yes

For a system at equilibrium, Q = Grand and ΔOne thousand = 0, and the previous equation may be written equally

[latex]0 = {\Delta}G^{\circ}\;+\;RT\;\text{ln}\;Yard\;\;\;\;\;\;\;(\text{at\;equilibrium})[/latex]

[latex]{\Delta}Chiliad^{\circ} = -RT\;\text{ln}\;K\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;K = east^{-\frac{{\Delta}One thousand^{\circ}}{RT}}[/latex]

This grade of the equation provides a useful link between these ii essential thermodynamic properties, and it can be used to derive equilibrium constants from standard gratis energy changes and vice versa. The relations between standard free free energy changes and equilibrium constants are summarized in Table 6.

K	ΔG°	Comments
> 1	< 0	Products are more than abundant at equilibrium.
< 1	> 0	Reactants are more than abundant at equilibrium.
= ane	= 0	Reactants and products are equally abundant at equilibrium.
Table half dozen. Relations between Standard Free Energy Changes and Equilibrium Constants

Example vi

Computing an Equilibrium Constant using Standard Gratis Energy Change
Given that the standard free energies of germination of Ag⁺(aq), Cl⁻(aq), and AgCl(s) are 77.1 kJ/mol, −131.2 kJ/mol, and −109.8 kJ/mol, respectively, calculate the solubility production, K _sp, for AgCl.

Solution
The reaction of interest is the following:

[latex]\text{AgCl}(s)\;{\rightleftharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = [\text{Ag}^{+}][\text{Cl}^{-}][/latex]

The standard free free energy modify for this reaction is get-go computed using standard gratuitous energies of germination for its reactants and products:

[latex]{\Delta}G^{\circ} = {\Delta}G_{298}^{\circ} = [{\Delta}G_{\text{f}}^{\circ}\;(\text{Ag}^{+}(aq))\;+\;{\Delta}G_{\text{f}}^{\circ}\;(\text{Cl}^{-}(aq))]\;-\;[{\Delta}G_{\text{f}}^{\circ}\;(\text{AgCl}(s))] = [77.ane\;\text{kJ/mol}\;-\;131.two\;\text{kJ/mol}]\;-\;[-109.8\;\text{kJ/mol}] = 55.7\;\text{kJ/mol}[/latex]

The equilibrium constant for the reaction may then exist derived from its standard free energy modify:

[latex]K_{\text{sp}} = east^{-\frac{{\Delta}Thou^{\circ}}{RT}} = \text{exp}\;(-\frac{{\Delta}Grand^{\circ}}{RT}) = \text{exp}(-\frac{55.7\;\times\;10^3\text{J/mol}}{8.314\;\text{J/mol}{\cdot}\text{1000}\;\times\;298.15\;\text{1000}}) = \text{exp}(-22.470) = eastward^{-22.470} = 1.74\;\times\;x^{-10}[/latex]

This result is in reasonable agreement with the value provided in Appendix J.

Check Your Learning
Use the thermodynamic information provided in Appendix One thousand to calculate the equilibrium constant for the dissociation of dinitrogen tetroxide at 25 °C.

[latex]2\text{NO}_2(grand)\;{\rightleftharpoons}\;\text{Northward}_2\text{O}_4(g)[/latex]

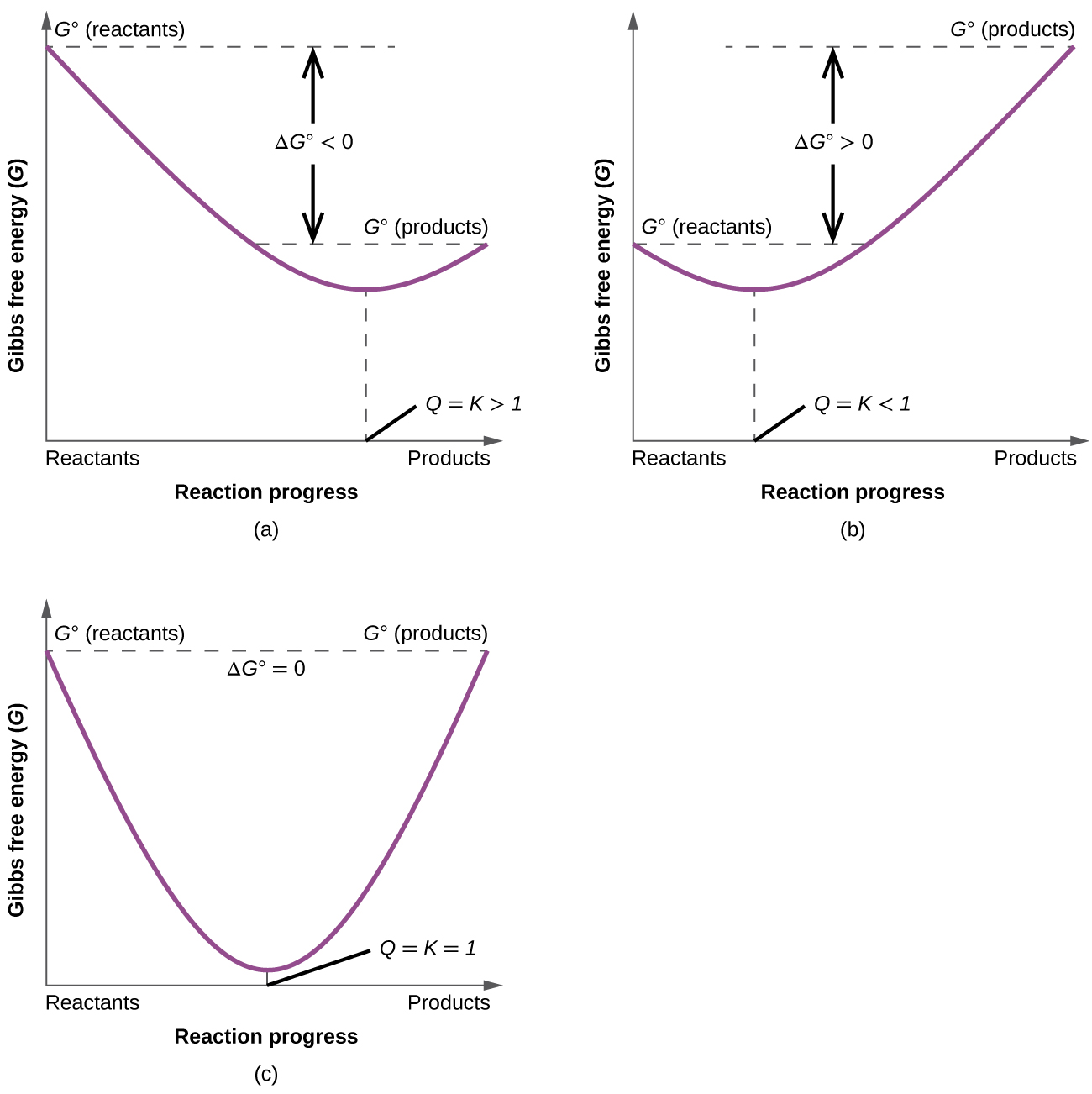
To further illustrate the relation between these ii essential thermodynamic concepts, consider the ascertainment that reactions spontaneously continue in a management that ultimately establishes equilibrium. As may be shown past plotting the complimentary energy alter versus the extent of the reaction (for example, as reflected in the value of Q), equilibrium is established when the system'southward complimentary free energy is minimized (Figure 3). If a system is present with reactants and products present in nonequilibrium amounts (Q ≠ K), the reaction will proceed spontaneously in the direction necessary to found equilibrium.

Effigy three. These plots show the gratis free energy versus reaction progress for systems whose standard free changes are (a) negative, (b) positive, and (c) zero. Nonequilibrium systems will proceed spontaneously in whatever management is necessary to minimize free free energy and constitute equilibrium.

Cardinal Concepts and Summary

Gibbs costless energy (G) is a state part defined with regard to system quantities just and may exist used to predict the spontaneity of a process. A negative value for ΔG indicates a spontaneous process; a positive Δ1000 indicates a nonspontaneous process; and a ΔG of zero indicates that the organisation is at equilibrium. A number of approaches to the ciphering of free energy changes are possible.

Key Equations

• ΔG = ΔH − TΔS
• ΔG = ΔGrand° + RT ln Q
• ΔG° = −RT ln K

Chemistry End of Chapter Exercises

1. What is the difference betwixt ΔG, ΔK°, and [latex]{\Delta}G_{298}^{\circ}[/latex] for a chemic modify?
2. A reactions has [latex]{\Delta}H_{298}^{\circ} = 100\;\text{kJ/mol}[/latex] and [latex]{\Delta}S_{298}^{\circ} = 250\;\text{J/mol}{\cdot}\text{K}[/latex]. Is the reaction spontaneous at room temperature? If not, under what temperature weather will it become spontaneous?
3. Explain what happens as a reaction starts with ΔG < 0 (negative) and reaches the signal where Δ1000 = 0.
4. Apply the standard complimentary free energy of formation information in Appendix Thousand to determine the free energy change for each of the following reactions, which are run under standard state conditions and 25 °C. Identify each as either spontaneous or nonspontaneous at these conditions.

   (a) [latex]\text{MnO}_2(s)\;{\longrightarrow}\;\text{Mn}(s)\;+\;\text{O}_2(g)[/latex]

   (b) [latex]\text{H}_2(g)\;+\;\text{Br}_2(l)\;{\longrightarrow}\;two\text{HBr}(g)[/latex]

   (c) [latex]\text{Cu}(s)\;+\;\text{S}(g)\;{\longrightarrow}\;\text{CuS}(due south)[/latex]

   (d) [latex]2\text{LiOH}(s)\;+\;\text{CO}_2(g)\;{\longrightarrow}\;\text{Li}_2\text{CO}_3(due south)\;+\;\text{H}_2\text{O}(k)[/latex]

   (e) [latex]\text{CH}_4(g)\;+\;\text{O}_2(g)\;{\longrightarrow}\;\text{C}(s\text{,\;graphite})\;+\;2\text{H}_2\text{O}(chiliad)[/latex]

   (f) [latex]\text{CS}_2(g)\;+\;3\text{Cl}_2(grand)\;{\longrightarrow}\;\text{CCl}_4(g)\;+\;\text{Southward}_2\text{Cl}_2(chiliad)[/latex]

5. Use the standard free energy information in Appendix 1000 to make up one's mind the complimentary energy alter for each of the post-obit reactions, which are run under standard land weather condition and 25 °C. Place each equally either spontaneous or nonspontaneous at these conditions.

   (a) [latex]\text{C}(s\text{,\;graphite})\;+\;\text{O}_2(one thousand)\;{\longrightarrow}\;\text{CO}_2(g)[/latex]

   (b) [latex]\text{O}_2(g)\;+\;\text{N}_2(m)\;{\longrightarrow}\;ii\text{NO}(g)[/latex]

   (c) [latex]two\text{Cu}(s)\;+\;\text{Southward}(m)\;{\longrightarrow}\;\text{Cu}_2\text{South}(s)[/latex]

   (d) [latex]\text{CaO}(s)\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{Ca(OH)}_2(s)[/latex]

   (e) [latex]\text{Iron}_2\text{O}_3(southward)\;+\;3\text{CO}(yard)\;{\longrightarrow}\;2\text{Fe}(s)\;+\;3\text{CO}_2(thou)[/latex]

   (f) [latex]\text{CaSO}_4\;{\cdot}\;2\text{H}_2\text{O}(s)\;{\longrightarrow}\;\text{CaSO}_4(s)\;+\;2\text{H}_2\text{O}(chiliad)[/latex]

6. Given:
   [latex]\brainstorm{array}{ll} \text{P}_4(s)\;+\;v\text{O}_2(g)\;{\longrightarrow}\;\text{P}_4\text{O}_{10}(south) & {\Delta}G_{298}^{\circ} = -2697.0\;\text{kJ/mol} \\[0.5em] 2\text{H}_2(g)\;+\;\text{O}_2(g)\;{\longrightarrow}\;2\text{H}_2\text{O}(k) & {\Delta}G_{298}^{\circ} = -457.18\;\text{kJ/mol} \\[0.5em] six\text{H}_2\text{O}(g)\;+\;\text{P}_4\text{O}_{10}(thou)\;{\longrightarrow}\;4\text{H}_3\text{PO}_4(fifty) & {\Delta}G_{298}^{\circ} = -428.66\;\text{kJ/mol} \cease{array}[/latex]

   (a) Make up one's mind the standard gratuitous energy of formation, [latex]{\Delta}G_{\text{f}}^{\circ}[/latex], for phosphoric acrid.

   (b) How does your calculated result compare to the value in Appendix G? Explain.

7. Is the formation of ozone (O_three(g)) from oxygen (O₂(thousand)) spontaneous at room temperature under standard state weather?
8. Consider the decomposition of cerise mercury(Ii) oxide under standard state weather.
   [latex]2\text{HgO}(due south\text{,\;ruddy})\;{\longrightarrow}\;2\text{Hg}(l)\;+\;\text{O}_2(g)[/latex]

   (a) Is the decomposition spontaneous under standard country conditions?

   (b) Above what temperature does the reaction go spontaneous?

9. Among other things, an ideal fuel for the control thrusters of a infinite vehicle should decompose in a spontaneous exothermic reaction when exposed to the appropriate goad. Evaluate the following substances under standard land conditions as suitable candidates for fuels.

   (a) Ammonia: [latex]2\text{NH}_3(g)\;{\longrightarrow}\;\text{N}_2(thousand)\;+\;three\text{H}_2(chiliad)[/latex]

   (b) Diborane: [latex]\text{B}_2\text{H}_6(yard)\;{\longrightarrow}\;2\text{B}(g)\;+\;3\text{H}_2(one thousand)[/latex]

   (c) Hydrazine: [latex]\text{Due north}_2\text{H}_4(k)\;{\longrightarrow}\;\text{N}_2(m)\;+\;2\text{H}_2(g)[/latex]

   (d) Hydrogen peroxide: [latex]\text{H}_2\text{O}_2(l)\;{\longrightarrow}\;\text{H}_2\text{O}(g)\;+\;\frac{one}{ii}\text{O}_2(one thousand)[/latex]

10. Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given.

    (a) [latex]\text{North}_2(yard)\;+\;\text{O}_2(g)\;{\longrightarrow}\;2\text{NO}(chiliad)\;\;\;\;\;\;\;\text{T} = 2000\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 4.ane\;\times\;10^{-iv}[/latex]

    (b) [latex]\text{H}_2(grand)\;+\;\text{I}_2(one thousand)\;{\longrightarrow}\;2\text{How-do-you-do}(one thousand)\;\;\;\;\;\;\;\text{T} = 400\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 50.0[/latex]

    (c) [latex]\text{CO}_2(1000)\;+\;\text{H}_2(g)\;{\longrightarrow}\;\text{CO}(thousand)\;+\;\text{H}_2\text{O}(yard)\;\;\;\;\;\;\;\text{T} = 980\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 1.67[/latex]

    (d) [latex]\text{CaCO}_3(south)\;{\longrightarrow}\;\text{CaO}(s)\;+\;\text{CO}_2(chiliad)\;\;\;\;\;\;\;\text{T} = 900\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 1.04[/latex]

    (e) [latex]\text{HF}(aq)\;+\;\text{H}_2\text{O}(fifty)\;{\longrightarrow}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{F}^{-}(aq)\;\;\;\;\;\;\;\text{T} = 25\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 7.2\;\times\;10^{-four}[/latex]

    (f) [latex]\text{AgBr}(s)\;{\longrightarrow}\;\text{Ag}^{+}(aq)\;+\;\text{Br}^{-}(aq)\;\;\;\;\;\;\;\text{T} = 25\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 3.3\;\times\;10^{-xiii}[/latex]

11. Summate ΔG° for each of the post-obit reactions from the equilibrium constant at the temperature given.

    (a) [latex]\text{Cl}_2(grand)\;+\;\text{Br}_2(g)\;{\longrightarrow}\;2\text{BrCl}(m)\;\;\;\;\;\;\;\text{T} = 25\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = iv.vii\;\times\;10^{-2}[/latex]

    (b) [latex]2\text{Then}_2(g)\;+\;\text{O}_2(1000)\;{\leftrightharpoons}\;2\text{SO}_3(g)\;\;\;\;\;\;\;\text{T} = 500\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 48.2[/latex]

    (c) [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;\;\;\;\;\;\;\text{T} = 60\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 0.196\;\text{atm}[/latex]

    (d) [latex]\text{CoO}(s)\;+\;\text{CO}(g)\;{\rightleftharpoons}\;\text{Co}(southward)\;+\;\text{CO}_2(1000)\;\;\;\;\;\;\;\text{T} = 550\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 4.90\;\times\;10^2[/latex]

    (eastward) [latex]\text{CH}_3\text{NH}_2(aq)\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{CH}_3\text{NH}_3^{+}(aq)\;+\;\text{OH}^{-}(aq)\;\;\;\;\;\;\;\text{T} = 25\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 4.4\;\times\;10^{-4}[/latex]

    (f) [latex]\text{PbI}_2(s)\;{\longrightarrow}\;\text{Pb}^{ii+}(aq)\;+\;2\text{I}^{-}(aq)\;\;\;\;\;\;\;\text{T} = 25\;^{\circ}\text{C}\;\;\;\;\;\;\;K_{\text{p}} = 8.7\;\times\;ten^{-9}[/latex]

12. Summate the equilibrium constant at 25 °C for each of the following reactions from the value of Δ1000° given.

    (a) [latex]\text{O}_2(grand)\;+\;2\text{F}_2(g)\;{\longrightarrow}\;2\text{OF}_2(chiliad)\;\;\;\;\;\;\;{\Delta}G^{\circ} = -ix.two\;\text{kJ}[/latex]

    (b) [latex]\text{I}_2(southward)\;+\;\text{Br}_2(l)\;{\longrightarrow}\;2\text{IBr}(g)\;\;\;\;\;\;\;{\Delta}G^{\circ} = vii.3\;\text{kJI}[/latex]

    (c) [latex]two\text{LiOH}(southward)\;+\;\text{CO}_2(g)\;{\longrightarrow}\;\text{Li}_2\text{CO}_3(s)\;+\;\text{H}_2\text{O}(thou)\;\;\;\;\;\;\;{\Delta}G^{\circ} = -79\;\text{kJ}[/latex]

    (d) [latex]\text{N}_2\text{O}_3(g)\;{\longrightarrow}\;\text{NO}(g)\;+\;\text{NO}_2(one thousand)\;\;\;\;\;\;\;{\Delta}G^{\circ} = -1.6\;\text{kJ}[/latex]

    (e) [latex]\text{SnCl}_4(fifty)\;{\longrightarrow}\;\text{SnCl}_4(l)\;\;\;\;\;\;\;{\Delta}Chiliad^{\circ} = 8.0\;\text{kJ}[/latex]

13. Calculate the equilibrium abiding at 25 °C for each of the following reactions from the value of ΔYard° given.

    (a) [latex]\text{I}_2(s)\;+\;\text{Cl}_2(one thousand)\;{\longrightarrow}\;2\text{ICl}(g)\;\;\;\;\;\;\;{\Delta}G^{\circ} = -10.88\;\text{kJ}[/latex]

    (b) [latex]\text{H}_2(g)\;+\;\text{I}_2(s)\;{\longrightarrow}\;2\text{How-do-you-do}(g)\;\;\;\;\;\;\;{\Delta}Chiliad^{\circ} = 3.4\;\text{kJ}[/latex]

    (c) [latex]\text{CS}_2(g)\;+\;iii\text{Cl}_2(one thousand)\;{\longrightarrow}\;\text{CCl}_4(g)\;+\;\text{S}_2\text{Cl}_2(one thousand)\;\;\;\;\;\;\;{\Delta}Chiliad^{\circ} = -39\;\text{kJ}[/latex]

    (d) [latex]two\text{And then}_2(g)\;+\;\text{O}_2(m)\;{\longrightarrow}\;ii\text{Then}_3(g)\;\;\;\;\;\;\;{\Delta}G^{\circ} = -141.82\;\text{kJ}[/latex]

    (e) [latex]\text{CS}_2(one thousand)\;{\longrightarrow}\;\text{CS}_2(l)\;\;\;\;\;\;\;{\Delta}G^{\circ} = -1.88\;\text{kJ}[/latex]

14. Summate the equilibrium constant at the temperature given.

    (a) [latex]\text{O}_2(g)\;+\;2\text{F}_2(grand)\;{\longrightarrow}\;ii\text{F}_2\text{O}(g)\;\;\;\;\;\;\;(\text{T} = 100\;^{\circ}\text{C})[/latex]

    (b) [latex]\text{I}_2(s)\;+\;\text{Br}_2(l)\;{\longrightarrow}\;2\text{IBr}(g)\;\;\;\;\;\;\;(\text{T} = 0.0\;^{\circ}\text{C})[/latex]

    (c) [latex]ii\text{LiOH}(s)\;+\;\text{CO}_2(g)\;{\longrightarrow}\;\text{Li}_2\text{CO}_3(southward)\;+\;\text{H}_2\text{O}(g)\;\;\;\;\;\;\;(\text{T} = 575\;^{\circ}\text{C})[/latex]

    (d) [latex]\text{North}_2\text{O}_3(m)\;{\longrightarrow}\;\text{NO}(grand)\;+\;\text{NO}_2(g)\;\;\;\;\;\;\;(\text{T} = -ten.0\;^{\circ}\text{C})[/latex]

    (east) [latex]\text{SnCl}_4(fifty)\;{\longrightarrow}\;\text{SnCl}_4(thou)\;\;\;\;\;\;\;(\text{T} = 200\;^{\circ}\text{C})[/latex]

15. Calculate the equilibrium constant at the temperature given.

    (a) [latex]\text{I}_2(s)\;+\;\text{Cl}_2(g)\;{\longrightarrow}\;2\text{ICl}(m)\;\;\;\;\;\;\;(\text{T} = 100\;^{\circ}\text{C})[/latex]

    (b) [latex]\text{H}_2(g)\;+\;\text{I}_2(s)\;{\longrightarrow}\;2\text{HI}(g)\;\;\;\;\;\;\;(\text{T} = 0.0\;^{\circ}\text{C})[/latex]

    (c) [latex]\text{CS}_2(1000)\;+\;3\text{Cl}_2(yard)\;{\longrightarrow}\;\text{CCl}_4(g)\;+\;\text{S}_2\text{Cl}_2(g)\;\;\;\;\;\;\;(\text{T} = 125\;^{\circ}\text{C})[/latex]

    (d) [latex]2\text{Then}_2(g)\;+\;\text{O}_2(g)\;{\longrightarrow}\;ii\text{SO}_3(g)\;\;\;\;\;\;\;(\text{T} = 675\;^{\circ}\text{C})[/latex]

    (e) [latex]\text{CS}_2(k)\;{\longrightarrow}\;\text{CS}_2(50)\;\;\;\;\;\;\;(\text{T} = ninety\;^{\circ}\text{C})[/latex]

16. Consider the following reaction at 298 K:
    [latex]\text{Northward}_2\text{O}_4(grand)\;{\rightleftharpoons}\;2\text{NO}_2(g)\;\;\;\;\;\;\;K_{\text{P}} = 0.142[/latex]

    What is the standard free energy change at this temperature? Describe what happens to the initial organisation, where the reactants and products are in standard states, as it approaches equilibrium.

17. Determine the normal boiling point (in kelvin) of dichloroethane, CH_iiCl₂. Find the actual boiling point using the Net or some other source, and calculate the percent mistake in the temperature. Explain the differences, if whatsoever, betwixt the two values.
18. Under what weather condition is [latex]\text{N}_2\text{O}_3(yard)\;{\longrightarrow}\;\text{NO}(yard)\;+\;\text{NO}_2(g)[/latex] spontaneous?
19. At room temperature, the equilibrium abiding (1000_w ) for the self-ionization of h2o is ane.00 × 10⁻¹⁴. Using this information, calculate the standard complimentary energy change for the aqueous reaction of hydrogen ion with hydroxide ion to produce h2o. (Hint: The reaction is the contrary of the self-ionization reaction.)
20. Hydrogen sulfide is a pollutant institute in natural gas. Post-obit its removal, it is converted to sulfur past the reaction [latex]2\text{H}_2\text{S}(g)\;+\;\text{SO}_2(g)\;{\rightleftharpoons}\;\frac{3}{viii}\text{South}_8(south\text{,\;rhombic})\;+\;two\text{H}_2\text{O}(l)[/latex]. What is the equilibrium constant for this reaction? Is the reaction endothermic or exothermic?
21. Consider the decomposition of CaCO₃(due south) into CaO(southward) and CO₂(thou). What is the equilibrium partial pressure of CO₂ at room temperature?
22. In the laboratory, hydrogen chloride (HCl(g)) and ammonia (NH_three(g)) oft escape from bottles of their solutions and react to form the ammonium chloride (NH_fourCl(s)), the white glaze oft seen on glassware. Assuming that the number of moles of each gas that escapes into the room is the same, what is the maximum partial pressure of HCl and NH₃ in the laboratory at room temperature? (Hint: The partial pressures will exist equal and are at their maximum value when at equilibrium.)
23. Benzene can be prepared from acetylene. [latex]3\text{C}_2\text{H}_2(m)\;{\rightleftharpoons}\;\text{C}_6\text{H}_6(one thousand)[/latex]. Determine the equilibrium constant at 25 °C and at 850 °C. Is the reaction spontaneous at either of these temperatures? Why is all acetylene not institute as benzene?
24. Carbon dioxide decomposes into CO and O_ii at elevated temperatures. What is the equilibrium partial pressure of oxygen in a sample at 1000 °C for which the initial pressure of CO₂ was 1.15 atm?
25. Carbon tetrachloride, an important industrial solvent, is prepared by the chlorination of methane at 850 K.
    [latex]\text{CH}_4(g)\;+\;4\text{Cl}_2(g)\;{\longrightarrow}\;\text{CCl}_4(m)\;+\;iv\text{HCl}(thousand)[/latex]

    What is the equilibrium constant for the reaction at 850 K? Would the reaction vessel demand to be heated or cooled to keep the temperature of the reaction constant?

26. Acetic acid, CH₃CO_twoH, can form a dimer, (CH₃CO₂H)_ii, in the gas phase.
    [latex]2\text{CH}_3\text{CO}_2\text{H}(1000)\;{\longrightarrow}\;(\text{CH}_3\text{CO}_2\text{H})_2(g)[/latex]

    The dimer is held together by ii hydrogen bonds with a total strength of 66.5 kJ per mole of dimer.
    

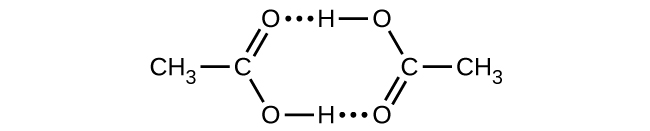
    At 25 °C, the equilibrium constant for the dimerization is 1.three × 10³ (force per unit area in atm). What is ΔSouthward° for the reaction?

27. Nitric acid, HNO_iii, tin can be prepared by the following sequence of reactions:
    [latex]4\text{NH}_3(g)\;+\;5\text{O}_2(g)\;{\longrightarrow}\;4\text{NO}(g)\;+\;six\text{H}_2\text{O}(m)[/latex]
    [latex]2\text{NO}(grand)\;+\;\text{O}_2(grand)\;{\longrightarrow}\;two\text{NO}_2(grand)[/latex]
    [latex]three\text{NO}_2(g)\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;2\text{HNO}_3(l)\;+\;\text{NO}(g)[/latex]

    How much heat is evolved when 1 mol of NH_three(one thousand) is converted to HNO₃(50)? Assume standard states at 25 °C.

28. Determine ΔYard for the following reactions.

    (a) Antimony pentachloride decomposes at 448 °C. The reaction is:

    [latex]\text{SbCl}_5(g)\;{\longrightarrow}\;\text{SbCl}_3(g)\;+\;\text{Cl}_2(g)[/latex]

    An equilibrium mixture in a v.00 50 flask at 448 °C contains 3.85 thousand of SbCl_five, 9.14 m of SbCl₃, and ii.84 g of Cl_ii.

    (b) Chlorine molecules dissociate according to this reaction:

    [latex]\text{Cl}_2(g)\;{\longrightarrow}\;2\text{Cl}(1000)[/latex]

    1.00% of Cl₂ molecules dissociate at 975 K and a pressure of 1.00 atm.

29. Given that the [latex]{\Delta}G_{\text{f}}^{\circ}[/latex] for Pb^two+(aq) and Cl⁻(aq) is −24.3 kJ/mole and −131.2 kJ/mole respectively, determine the solubility product, K _sp, for PbCl_two(s).
30. Make up one's mind the standard free energy alter, [latex]{\Delta}G_{\text{f}}^{\circ}[/latex], for the germination of S²⁻(aq) given that the [latex]{\Delta}G_{\text{f}}^{\circ}[/latex] for Ag⁺(aq) and Ag_iiSouthward(southward) are 77.1 g/mole and −39.5 kJ/mole respectively, and the solubility product for Ag₂S(south) is 8 × x⁻⁵¹.
31. Determine the standard enthalpy change, entropy alter, and costless energy change for the conversion of diamond to graphite. Hash out the spontaneity of the conversion with respect to the enthalpy and entropy changes. Explicate why diamond spontaneously irresolute into graphite is not observed.
32. The evaporation of one mole of water at 298 K has a standard free energy modify of 8.58 kJ.
    [latex]\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;\text{H}_2\text{O}(g)\;\;\;\;\;\;\;{\Delta}G_{298}^{\circ} = 8.58\;\text{kJ}[/latex]

    (a) Is the evaporation of water under standard thermodynamic conditions spontaneous?

    (b) Determine the equilibrium constant, K_P , for this physical process.

    (c) By calculating ∆K, determine if the evaporation of h2o at 298 K is spontaneous when the partial force per unit area of water, [latex]\text{P}_{\text{H}_2\text{O}}[/latex], is 0.011 atm.

    (d) If the evaporation of water were e'er nonspontaneous at room temperature, wet laundry would never dry when placed exterior. In order for laundry to dry, what must exist the value of [latex]\text{P}_{\text{H}_2\text{O}}[/latex] in the air?

33. In glycolysis, the reaction of glucose (Glu) to course glucose-6-phosphate (G6P) requires ATP to exist present as described by the following equation:
    [latex]\text{Glu}\;+\;\text{ATP}\;{\longrightarrow}\;\text{G}6\text{P}\;+\;\text{ADP}\;\;\;\;\;\;\;{\Delta}G_{298}^{\circ} = -17\;\text{kJ}[/latex]

    In this process, ATP becomes ADP summarized past the following equation:

    [latex]\text{ATP}\;{\longrightarrow}\;\text{ADP}\;\;\;\;\;\;\;{\Delta}G_{298}^{\circ} = -thirty\;\text{kJ}[/latex]

    Determine the standard gratuitous energy change for the post-obit reaction, and explain why ATP is necessary to drive this process:

    [latex]\text{Glu}\;{\longrightarrow}\;\text{One thousand}6\text{P}\;\;\;\;\;\;\;{\Delta}G_{298}^{\circ} = \text{?}[/latex]

34. One of the important reactions in the biochemical pathway glycolysis is the reaction of glucose-half dozen-phosphate (G6P) to course fructose-6-phosphate (F6P):
    [latex]\text{G}six\text{P}\;{\leftrightharpoons}\;\text{F}half dozen\text{P}\;\;\;\;\;\;\;{\Delta}G_{298}^{\circ} = 1.7\;\text{kJ}[/latex]

    (a) Is the reaction spontaneous or nonspontaneous under standard thermodynamic conditions?

    (b) Standard thermodynamic conditions imply the concentrations of G6P and F6P to exist ane M, however, in a typical cell, they are non fifty-fifty close to these values. Calculate ΔG when the concentrations of G6P and F6P are 120 μM and 28 μM respectively, and discuss the spontaneity of the forwards reaction under these atmospheric condition. Assume the temperature is 37 °C.

35. Without doing a numerical calculation, determine which of the post-obit will reduce the free energy change for the reaction, that is, get in less positive or more negative, when the temperature is increased. Explain.

    (a) [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\longrightarrow}\;ii\text{NH}_3(one thousand)[/latex]

    (b) [latex]\text{HCl}(g)\;+\;\text{NH}_3(m)\;{\longrightarrow}\;\text{NH}_4\text{Cl}(s)[/latex]

    (c) [latex](\text{NH}_4)_2\text{Cr}_2\text{O}_7(due south)\;{\longrightarrow}\;\text{Cr}_2\text{O}_3(due south)\;+\;4\text{H}_2\text{O}(g)\;+\;\text{Due north}_2(g)[/latex]

    (d) [latex]ii\text{Fe}(s)\;+\;three\text{O}_2(g)\;{\longrightarrow}\;\text{Fe}_2\text{O}_3(southward)[/latex]

36. When ammonium chloride is added to water and stirred, it dissolves spontaneously and the resulting solution feels common cold. Without doing whatever calculations, deduce the signs of ΔG, ΔH, and ΔS for this process, and justify your choices.
37. An of import source of copper is from the copper ore, chalcocite, a course of copper(I) sulfide. When heated, the Cu₂S decomposes to form copper and sulfur described by the following equation:
    [latex]\text{Cu}_2\text{S}(s)\;{\longrightarrow}\;\text{Cu}(s)\;+\;\text{South}(s)[/latex]

    (a) Determine [latex]{\Delta}G_{298}^{\circ}[/latex] for the decomposition of Cu₂S(south).

    (b) The reaction of sulfur with oxygen yields sulfur dioxide equally the just product. Write an equation that describes this reaction, and determine [latex]{\Delta}G_{298}^{\circ}[/latex] for the process.

    (c) The production of copper from chalcocite is performed past roasting the Cu₂South in air to produce the Cu. Past combining the equations from Parts (a) and (b), write the equation that describes the roasting of the chalcocite, and explain why coupling these reactions together makes for a more than efficient process for the production of the copper.

38. What happens to [latex]{\Delta}G_{298}^{\circ}[/latex] (becomes more than negative or more positive) for the post-obit chemical reactions when the partial pressure of oxygen is increased?

    (a) [latex]\text{South}(s)\;+\;\text{O}_2(k)\;{\longrightarrow}\;\text{SO}_2(g)[/latex]

    (b) [latex]2\text{SO}_2(g)\;+\;\text{O}_2(g)\;{\longrightarrow}\;\text{SO}_3(g)[/latex]

    (c) [latex]\text{HgO}(s)\;{\longrightarrow}\;\text{Hg}(l)\;+\;\text{O}_2(g)[/latex]

Glossary

Gibbs free energy change (G)

thermodynamic belongings defined in terms of system enthalpy and entropy; all spontaneous processes involve a subtract in G

standard gratuitous energy change (ΔG°)

change in free energy for a process occurring nether standard atmospheric condition (one bar pressure for gases, ane M concentration for solutions)

standard energy of formation [latex](\Delta G^{^circ}_{\text{f}}[/latex]

change in costless energy accompanying the formation of one mole of substance from its elements in their standard states

Solutions

Answers to Chemical science Stop of Affiliate Exercises

ii. The reaction is nonspontaneous at room temperature.
Above 400 Thou, ΔThousand volition become negative, and the reaction will become spontaneous.

4. (a) 465.1 kJ nonspontaneous; (b) −106.86 kJ spontaneous; (c) −53.6 kJ spontaneous; (d) −83.4 kJ spontaneous; (due east) −406.7 kJ spontaneous; (f) −30.0 kJ spontaneous

6. (a) −1124.iii kJ/mol for the standard free energy alter. (b) The calculation agrees with the value in Appendix Grand considering free free energy is a state function (merely like the enthalpy and entropy), so its change depends only on the initial and final states, not the path betwixt them.

8. (a) The reaction is nonspontaneous; (b) Above 566 °C the process is spontaneous.

10. (a) 1.5 × 10² kJ; (b) −21.ix kJ; (c) −5.34 kJ; (d) −0.383 kJ; (e) eighteen kJ; (f) 71 kJ

12. (a) K = 41; (b) Thousand = 0.053; (c) M = 6.9 × ten^thirteen; (d) K = i.9; (due east) Thou = 0.04

14. In each of the following, the value of ΔK is non given at the temperature of the reaction. Therefore, we must calculate ΔG from the values ΔH° and ΔS and so calculate ΔG from the relation ΔThousand = ΔH° − TΔS°.

(a) K = 1.29;

(b) K = 2.51 × x⁻³;

(c) Grand = 4.83 × 10³;

(d) Yard = 0.219;

(due east) One thousand = 16.i

16. The standard complimentary energy change is [latex]{\Delta}G_{298}^{\circ} = -RT\;\text{ln}\;K = four.84\;\text{kJ/mol}[/latex]. When reactants and products are in their standard states (i bar or one atm), Q = 1. As the reaction proceeds toward equilibrium, the reaction shifts left (the corporeality of products drops while the corporeality of reactants increases): Q < i, and [latex]{\Delta}G_{298}[/latex] becomes less positive as information technology approaches cypher. At equilibrium, Q = K, and ΔK = 0.

18. The reaction will be spontaneous at temperatures greater than 287 K.

twenty. K = 5.35 × 10¹⁵
The procedure is exothermic.

22. 1.0 × x⁻⁸ atm. This is the maximum pressure of the gases nether the stated conditions.

24. [latex]x = 1.29\;\times\;10^{-5}\;\text{atm} = \text{P}_{\text{O}_2}[/latex]

26. −0.xvi kJ

28. (a) −22.1 kJ; (b) 61.6 kJ/mol

30. 90 kJ/mol

32. (a) Under standard thermodynamic weather, the evaporation is nonspontaneous; (b) K_p = 0.031; (c) The evaporation of h2o is spontaneous; (d) [latex]\text{P}_{\text{H}_2\text{O}}[/latex] must always be less than Grand_p or less than 0.031 atm. 0.031 atm represents air saturated with water vapor at 25 °C, or 100% humidity.

34. (a) Nonspontaneous equally [latex]{\Delta}G_{298}^{\circ}\;{\textgreater}\;0[/latex]; (b) [latex]{\Delta}G_{298}^{\circ} = -RT\;\text{ln}\;K\text{,\;}{\Delta}One thousand = ane.7\;\times\;10^3\;+\;(8.314\;\times\;335\;\times\;\text{ln}\;\frac{28}{128}) = -2.five\;\text{kJ}[/latex]. The forrad reaction to produce F6P is spontaneous under these atmospheric condition.

36. ΔYard is negative every bit the process is spontaneous. ΔH is positive equally with the solution becoming common cold, the dissolving must be endothermic. ΔS must be positive every bit this drives the process, and it is expected for the dissolution of any soluble ionic chemical compound.

38. (a) Increasing [latex]P_{\text{O}_2}[/latex] volition shift the equilibrium toward the products, which increases the value of K. [latex]{\Delta}G_{298}^{\circ}[/latex] therefore becomes more negative.
(b) Increasing [latex]P_{\text{O}_2}[/latex] will shift the equilibrium toward the products, which increases the value of K. [latex]{\Delta}G_{298}^{\circ}[/latex] therefore becomes more negative.
(c) Increasing [latex]P_{\text{O}_2}[/latex] will shift the equilibrium the reactants, which decreases the value of K. [latex]{\Delta}G_{298}^{\circ}[/latex] therefore becomes more positive.

bradleyantogginly.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/16-4-free-energy/

Share this post